这款需要多人作战的贪吃蛇游戏比起单机玩法增添了许多不一样的乐趣和挑战。贪吃蛇大作战怎么玩萌新攻略你想知道吗?下面让小编告诉你吧。
一、贪吃蛇大作战萌新怎么玩?
1、基本玩法
在游戏界面中,玩家的左手操作圈是用来进行移动和改变方位,右手边则是控制加速技能的释放和停止。加速技能的释放会消耗少量小蛇的长度,要注意控制技能的释放。
在吃掉彩色的豆子后小蛇的长度便会相应增加,但是要注意有的豆子在地图的边界,千万要注意别为了吃豆子而撞上边界,会导致小蛇死亡哦。
在地图中还会遇到其他玩家的小蛇,头部撞到其他小蛇也会导致死亡。要消灭敌蛇需要用身体去撞击,消灭后可吃下敌蛇的豆子来增加自身的长度。
2、模式玩法
在无尽模式中,没有最终的胜利,玩家可随时进入游戏中,在小蛇死亡后获得相应的长度奖励和杀敌奖励。
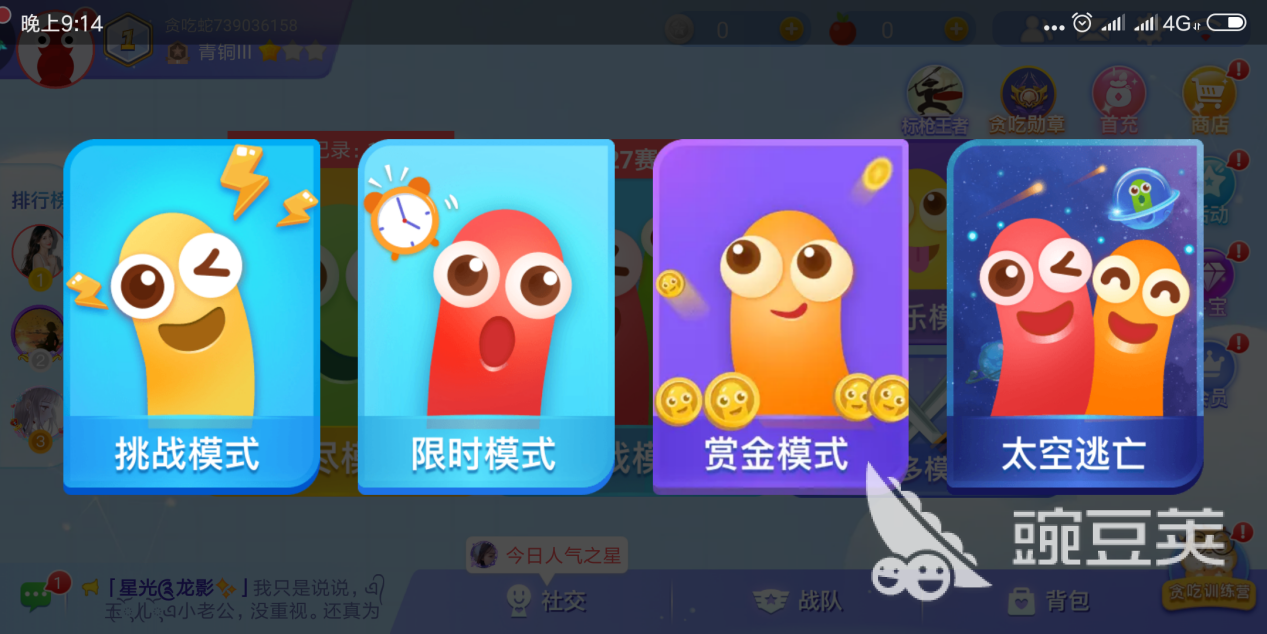
在娱乐模式中有着四种模式,分别是挑战模式、限时模式、赏金模式及太空逃亡。
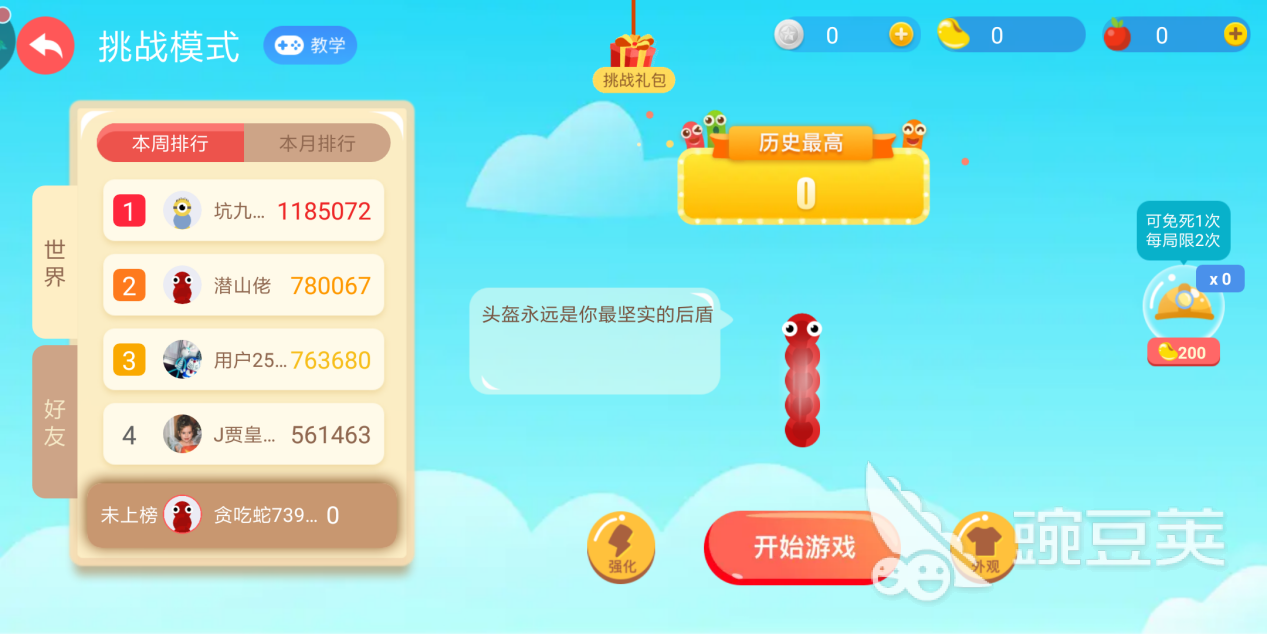
在挑战模式中,玩家在游戏中获得的金豆将用于道具的强化,而得分越高则最后结算时获得的金豆将越多。
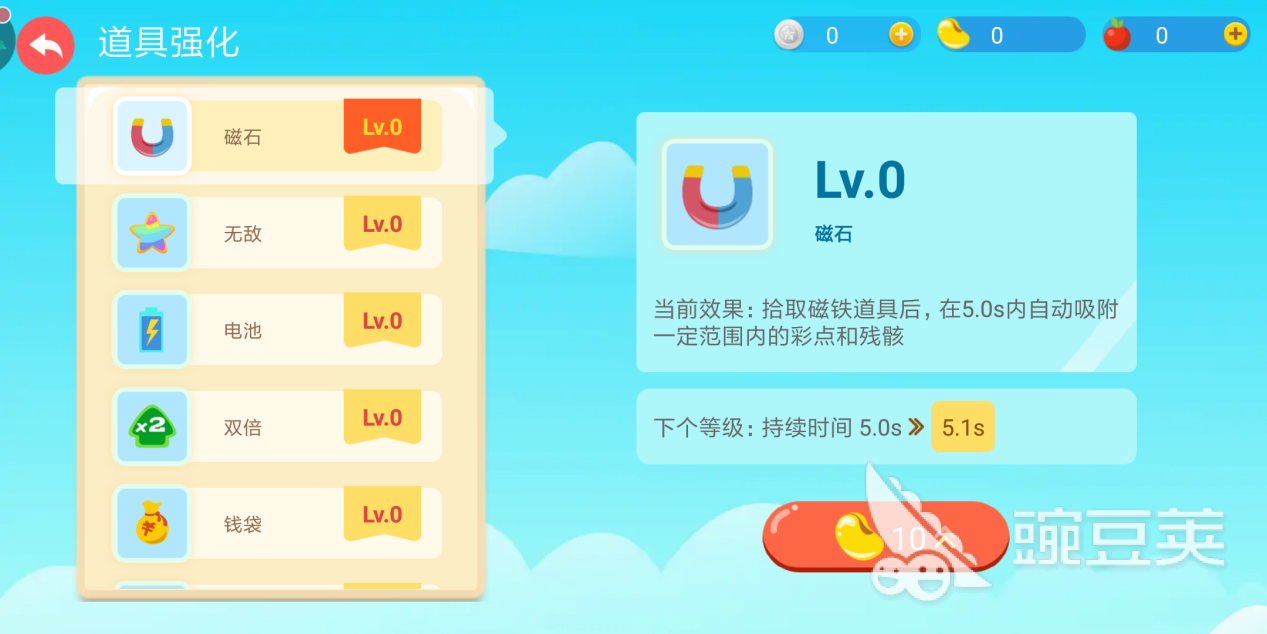
玩家在游戏中会获得一个强力技能,技能需要在击杀敌人后才能补充能力并进行释放,不同的技能作用不同玩家要记得仔细查看。同时在击杀一个敌人后进行连续击杀可以获得连击奖励哦。
限时模式的基本玩法等同于无尽模式,唯一不同的便是每局游戏有时长的限制,一局游戏五分钟。每局游戏结束都可获得积分奖励,积分每周有一定的上限。
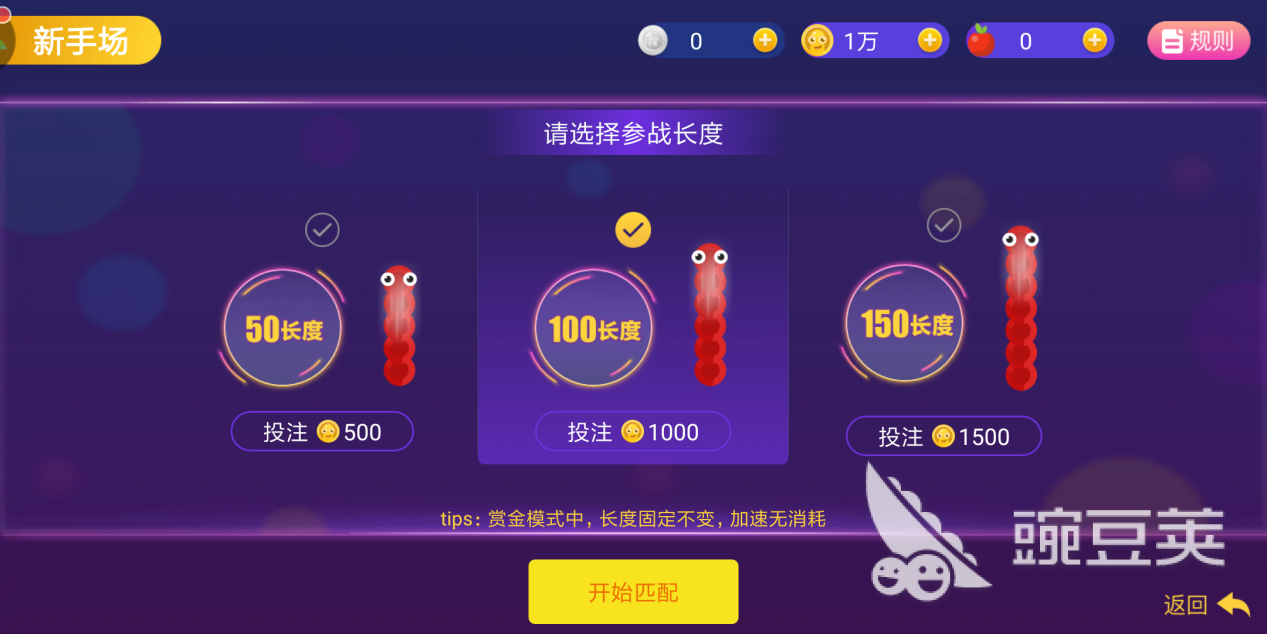
赏金模式的玩法是支付入场费进场,在支付入场费后选择参战长度并进行投注,长度和投注成正比。分别是50长度投注500、100长度投注1000、150长度投注1500。在赏金模式中,长度是固定不变的,使用加速技能不会对自身长度有消耗。
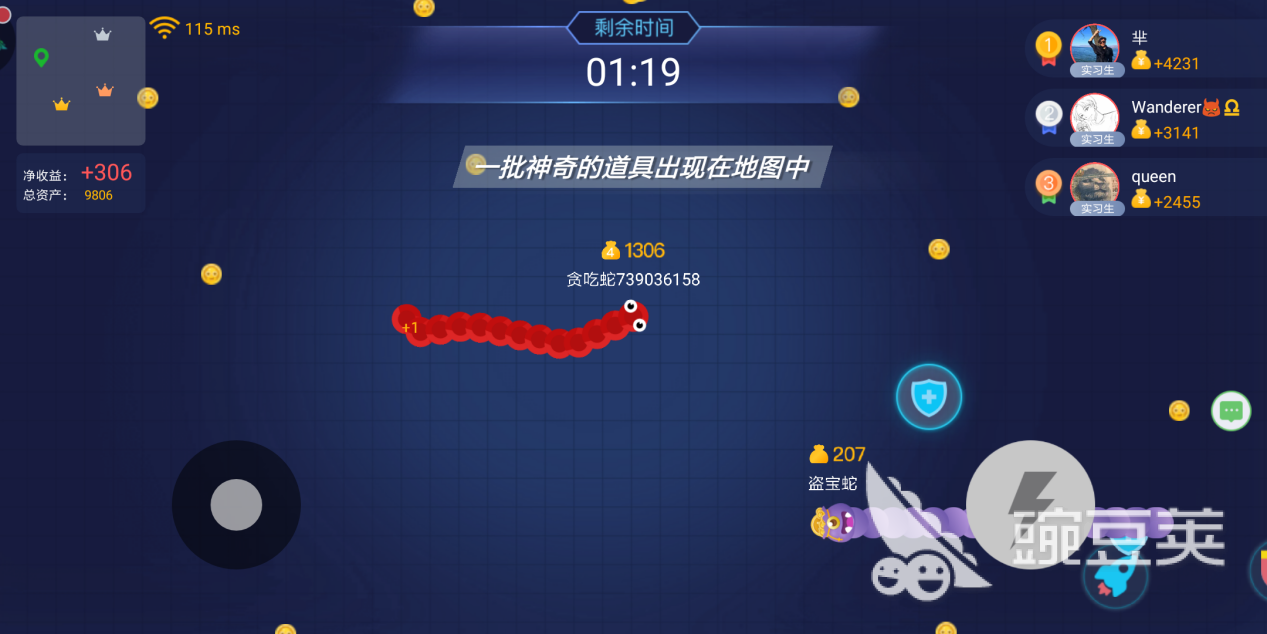
每局比赛中一共有十个玩家,一局时长为三分钟。玩家在收集欢乐币的同时也要注意别被其他玩家击杀,被击杀会失去所有已收集到的和本身投注的欢乐币。海盗蛇会携带大量欢乐币,要记得小心消灭对方。在游戏中还会随机刷新道具,要注意抢先下手。

在太空逃亡中玩家可以体验一把在太空中进行游戏的感觉。在这种模式中,安全区域会逐渐缩小,活到最后是唯一的目标。一局游戏中共有29名玩家,安全区为绿色,辐射区则为红色。小蛇的头部在辐射区会受到持续伤害,要注意躲避辐射伤害进入安全区。
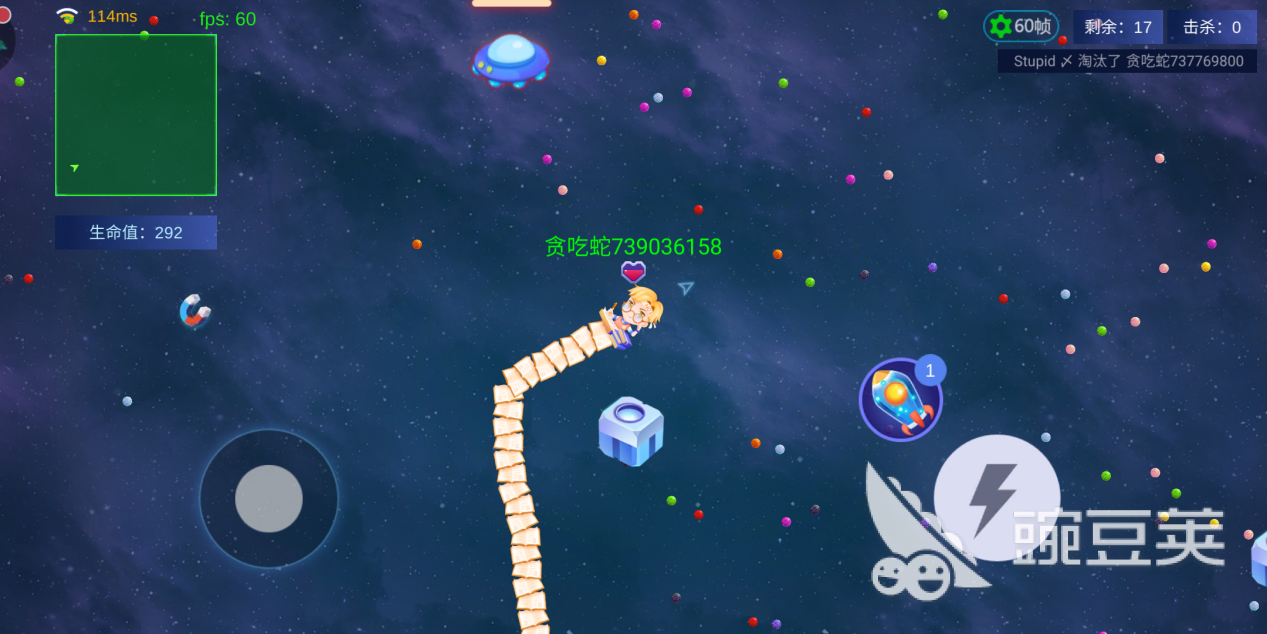
玩家在游戏开始时头顶会显示生命之心,进食可增加生命值,停留在辐射区会缓慢减少,而撞击到敌身则会扣除一颗。在地图中会随机散步一些宝箱,要记得避开敌人的同时去撞击并领取奖励。还要记得躲避敌人的导弹技能的攻击。
3、团战模式
在熟悉了基本玩法后,就可以进行团战模式的玩法了。在团战模式中,小蛇的头部撞到同队(同色)的队友不会死亡。
游戏中会随机刷新道具及BOSS,在拾取到护盾后要记得需手动释放才可获得5秒的无敌时间。而击杀BOSS后则是全队会获得加速提升,所以要记得强杀BOSS哦。

总长度率先达到4000分或加时赛结束时分数领先的队伍则可获得胜利。


